Graded: Supplemental #1, 7.2 #10

$\bigstar$ Supplemental #1

The largest integer not of the form $5s+7t$ (with $s,t\in\mathbb N$) is 23.

To prove that 23 is not of this form, we argue by contradiction. Suppose $5s+7t=23$, where $s,t\in\mathbb N$. Then $5s+7t\equiv 23\pmod 5$. Subtracting a multiple of 5 from each side, we have $2t\equiv 3\pmod 5$. The unique solution is $t\equiv 4\pmod 5$. Thus $t\ge 4$, but then $5s+7t\ge 28$, which is a contradiction. Therefore, $23\ne 5s+7t$ for $s,t\in\mathbb N$.

To prove that all integers greater than or equal to 24 are of the form $5s+7t$ with $s,t\in\mathbb N$, we argue by strong induction. The basis step is to show that 24 through 28 are of this form: \begin{align*} 24 &= 5(2)+7(2) \\ 25 &= 5(5)+7(0) \\ 26 &= 5(1)+7(3) \\ 27 &= 5(4)+7(1) \\ 28 &= 5(0)+7(4) \end{align*} For the inductive step, let $k\ge 29$ and suppose all integers from 24 to $k-1$ can be written in the form $5s+7t$ with $s,t\in\mathbb N$. In particular, $k-5=5s+7t$ for some $s,t\in\mathbb N$. Then $k=5(s+1)+7t$, where $s+1\in\mathbb N$ and $t\in\mathbb N$. This completes the inductive step, and we conclude that all integers greater than or equal to 24 are of the desired form. $\blacksquare$

Supplemental #2

Paths through the gapped grid can be thought of as paths through the complete grid below that don’t pass through point $C$: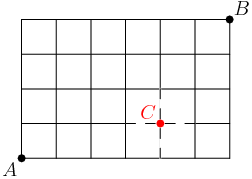We can count these by first counting all the paths from $A$ to $B$, then subtracting those that pass through $C$. There are $\binom{10}4=210$ paths from $A$ to $B$, because each such path must consist of 10 steps, of which any 4 can be “up” and the other 6 are “right”. There are $\binom 51\binom 53=5\cdot 10=50$ paths from $A$ to $C$ to $B$, since any of $\binom 51$ paths from $A$ to $C$ can be combined with any of $\binom 53$ paths from $C$ to $B$. Therefore, the gapped grid allows $210-50=\boxed{160}$ paths from $A$ to $B$.

Supplemental #3

There are 15 ways. Wolfram Alpha has the complete list.

Supplemental #4

We consider cases based on the number of objects distributed to each box. There are 15 such cases, per Supplemental Problem #3 above. The first few cases are presented in full detail below:

Case 1: 8 objects in one box. In this case, there are no choices to be made about which objects go to which box, so this case yields only 1 way of distributing 8 distinguishable objects.

Case 2: 7 objects in one box, 1 object in another box. In this case, there are $\frac{8!}{7!1!}$ ways to divide the objects between the two boxes.

Case 3: 6 objects in one box, 2 objects in another box. In this case, there are $\frac{8!}{6!2!}$ ways to divide the objects between the two boxes.

Case 4: 6 objects in one box, 1 object in a second box, and 1 object in a third box. In this case, there are $\frac{8!}{6!1!1!}$ ways to divide the objects among the three boxes, but this assumes the boxes are distinguishable. In fact, the second and third boxes are indistinguishable (each is to contain 1 object, so it makes no difference if we swap them). To avoid overcounting, we must divide by $2!$. Thus there are $\frac{8!}{6!1!1!2!}$ ways to distribute 8 distinguishable objects to indistinguishable boxes containing 6, 1, and 1 objects.

Based on the principles above, we now state the general rule. Let $n_1+n_2+\cdots+n_k=n$. The number of ways to distribute $n$ distinguishable objects to $k$ indistinguishable boxes such that the boxes receive $n_1,n_2,\ldots,n_k$ objects is $$\frac{n!}{n_1!n_2!\cdots n_k!~r_1!r_2!\cdots r_n!},$$ where $r_i$ is the number of times the value $i$ is repeated among the numbers $n_1,n_2,\ldots,n_k$.

Summing over all 15 cases, the number of ways to distribute 8 distinguishable objects to 4 indistinguishable boxes is $1+\frac{8!}{7!1!}+\frac{8!}{6!2!}+\frac{8!}{6!1!1!~2!}+\frac{8!}{5!3!}+\frac{8!}{5!2!1!}+\frac{8!}{5!1!1!1!~3!}+\frac{8!}{4!4!~2!}+\frac{8!}{4!3!1!}+\frac{8!}{4!2!2!~2!}+\frac{8!}{4!2!1!1!~2!}+\frac{8!}{3!3!2!~2!}+\frac{8!}{3!3!1!1!~2!2!}+\frac{8!}{3!2!2!1!~2!}+\frac{8!}{2!2!2!2!~4!}=\boxed{2795}$.

7.1 #10

There are $\binom{52}5$ equally probable hands (considering the order of the cards as irrelevant). The number of these hands containing the two of diamonds and the three of spades is $\binom{50}3$, because the three unspecified cards may be chosen freely from the other 50 cards in the deck. Therefore, the probability of drawing the two of diamonds and the three of spades in a given hand is $\dfrac{\binom{50}3}{\binom{52}5} = \dfrac{50!}{47!3!}\cdot\dfrac{47!5!}{52!} = \dfrac{5\cdot 4}{52\cdot 51} = \dfrac 5{663}$, or about $0.75\%$.

7.1 #14

In this problem, it is convenient to regard the cards in a hand as ordered. Then there are $P(52,5)=52\cdot 51\cdot 50\cdot 49\cdot 48$ possible hands. Of these, the number of hands in which no rank is repeated is $52\cdot 48\cdot 44\cdot 40\cdot 36$, since we can choose the first card in 52 ways, the second card in 48 ways (avoiding the 4 cards of the rank already chosen), etc. So the probability of drawing a hand with no repeated ranks is $\dfrac{52\cdot 48\cdot 44\cdot 40\cdot 36}{52\cdot 51\cdot 50\cdot 49\cdot 48} = \dfrac{2112}{4165}$, about $50.7\%$.

We can also solve the problem using unordered hands. The number of ways to form an unordered hand of five cards of different ranks is $\binom{13}5\cdot 4^5$, where $\binom{13}5$ is the number of ways to choose the ranks and $4^5$ is the number of ways to choose the suits. Thus the probability of drawing such a hand is $\dfrac{\binom{13}5\cdot 4^5}{\binom{52}5}$, which simplifies as above.

7.1 #36

When two dice are rolled, there are $6\cdot 6=36$ equally probable outcomes for the pair of resulting values. Of these, five pairs add up to 8, namely: (6,2), (5,3), (4,4), (3,5), (2,6). So the probability of rolling a total of 8 on two dice is $\frac 5{36}$.

When three dice are rolled, there are $6\cdot 6\cdot 6=216$ equally probable outcomes. We could exhaustively count the ways to roll a total of 8, but here is an alternative way. We wish to determine the number of triples $(x_1,x_2,x_3)$ such that $x_1,x_2,x_3$ are integers, $x_i\ge 1$ for $i=1,2,3$, $x_i\le 6$ for $i=1,2,3$, and $x_1+x_2+x_3=8$. The condition $x_i\le 6$ is redundant, because if each $x_i$ is at least 1, then no $x_i$ can be greater than $8-1-1=6$. Throwing out the redundant condition, we are now solving a familiar problem, which is equivalent to counting the ways to put 8 indistinguishable objects into 3 distinguishable boxes such that each box gets at least 1 object. We do this by putting 1 object in each box to start and then distributing the remaining 5 objects in any of $\binom{5+3-1}5=21$ ways. So there are 21 ways to roll a total of 8 on three dice.

To double-check the above, here is the exhaustive list: (6,1,1); (5,2,1); (5,1,2); (4,3,1); (4,2,2); (4,1,3); (3,4,1); (3,3,2); (3,2,3); (3,1,4); (2,5,1); (2,4,2); (2,3,3); (2,2,4); (2,1,5); (1,6,1); (1,5,2); (1,4,3); (1,3,4); (1,2,5); (1,1,6).

Yep, there are 21.

Thus the probability of rolling a total of 8 on three dice is $\frac{21}{216}$, which is less than $\frac 5{36}$. So we’re more likely to roll 8 on two dice.

7.1 #38

a) Yes, independent.

b) Yes, independent, though this is not obvious. The probability of $E_1$ is $\frac 12$. The probability of $E_2$ is $\frac 28$, because of the 8 series of three coin flips, two satisfy the description of $E_2$ (HHT, THH). The probability of $E_1\cap E_2$ is $\frac 18$, because the only series of coin flips that falls within both events is THH.

Since $p(E_1\cap E_2)=p(E_1)p(E_2)$, we conclude that events $E_1$ and $E_2$ are independent.

c) No, not independent. The probability of $E_1$ is $\frac 12$ and the probability of $E_2$ is $\frac 28$, but the probability of $E_1\cap E_2$ is 0, so $p(E_1\cap E_2)\ne p(E_1)p(E_2)$.

$\bigstar$ 7.2 #10

a) The probability is $\frac 1{13!}$, because alphabetical order is one of $13!$ equally likely orders the first 13 letters can be in.

Alternatively, of the $26!$ permutations, there are $\binom{26}{13}\cdot 13!$ in which the first 13 letters appear in alphabetical order (because we can choose the first 13 letters in $\binom{26}{13}$ ways, and choose how to order the remaining 13 letters in $13!$ ways). So the probability of the first 13 letters being in alphabetical order is $\frac{\binom{26}{13}\cdot 13!}{26!}$, which simplifies to $\frac 1{13!}$.

b) Of the $26!$ permutations, there are $24!$ that start with ‘a’ and end in ‘z’ (since the 24 letters in the middle can be ordered in any way). Thus the probability that a random permutation starts with ‘a’ and ends in ‘z’ is $\frac{24!}{26!}=\frac 1{26\cdot 25}=\frac 1{650}$.

Here is another approach that is well worth considering. Let $E_1$ be the event that the first letter is ‘a’. Let $E_2$ be the event that the last letter is ‘z’. Then $p(E_1)=\frac 1{26}$, because the first letter is equally likely to be any of the 26 letters. Also, $p(E_2~|~E_1)=\frac 1{25}$, because given that the first letter is ‘a’, there are 25 remaining letters which are equally likely to be in the last position. Thus $p(E_1\cap E_2) = p(E_1)p(E_2~|~E_1) = \frac 1{26}\cdot\frac 1{25} = \frac 1{650}$.

c) To form a permutation in which ‘a’ and ‘z’ are adjacent, we consider ‘az’ as a single letter. There are $25!$ ways to permute ‘az’,b,c,…,y. But ‘az’ can also appear as ‘za’, so the number of permutations in which ‘a’ and ‘z’ are adjacent is $25!\cdot 2!$. Thus the probability of obtaining such a permutation is $\frac{25!\cdot 2!}{26!} = \frac 2{26} = \frac 1{13}$.

d) By part (c), the probability that ‘a’ and ‘b’ are next to each other is $\frac 1{13}$, so the probability that they are not next to each other is $1-\frac 1{13} = \frac{12}{13}$.

e) “Separated by at least 23 letters” is somewhat ambiguous. In this solution, I have taken it to mean that there should be at least 23 letters between ‘a’ and ‘z’ (so the distance between ‘a’ and ‘z’ is at least 24). With this interpretation, there are three possible cases: (1) ‘a’ is the first letter and ‘z’ is the last letter, (2) ‘a’ is the first letter and ‘z’ is the 25th letter, (3) ‘a’ is the 2nd letter and ‘z’ is the last letter. Each of these cases occurs with probability $\frac 1{650}$, so the probability that ‘a’ and ‘z’ are separated by at least 23 letters is $\frac 3{650}$.

f) The probability is $\frac 13$, because whatever set of positions are occupied by the letters ‘a’, ‘b’, ‘z’, each of these letters is equally likely to be the first of the three.

7.2 #16

Suppose $E$ and $F$ are independent events. Then $p(E\cap F)=p(E)p(F)$.

To show that $\overline E$ and $\overline F$ are independent, it suffices to show that $p(\overline E\cap\overline F)=p(\overline E)p(\overline F)$.

By de Morgan’s laws, $\overline E\cap\overline F = \overline{E\cup F}$, so $$p(\overline E\cap\overline F) = 1-p(E\cup F).$$ By the general result $p(E\cup F) = p(E)+p(F)-p(E\cap F)$ (which is on p. 455 of the book), we now have \begin{align*} p(\overline E\cap\overline F) &= 1-p(E)-p(F)+p(E\cap F) \\ &= 1-p(E)-p(F)+p(E)p(F) \\ &= (1-p(E))(1-p(F)) \\ &= p(\overline E)p(\overline F), \end{align*} so $\overline E$ and $\overline F$ are independent events. $\blacksquare$

(Make sure you see where the hypothesis that $E,F$ are independent was used.)

7.2 #18

a) The probability is $\frac 17$, since the second person is equally likely to have been born on any of the seven days, one of which matches the first person.

b) If $2\le n\le 7$, the probability is $1-\left(\frac 67\cdot\frac 57\cdot~\cdots~\cdot\frac{8-n}7\right)$. If $n\ge 8$, the probability is 1.

c) With three people, the probability is about 39%; with four, it’s about 65%, so four people are enough.

7.2 #28

a) $\binom 53(0.51)^3(1-0.51)^2 \approx 31.8\%$

b) $1-(1-0.51)^5 \approx 97.2\%$

c) $1-(0.51)^5 \approx 96.5\%$

d) $(0.51)^5+(1-0.51)^5 \approx 6.3\%$

7.2 #38

a) There are 11 outcomes for the die roll that are consistent with the report of the honest observer: (1,6), (2,6), (3,6), (4,6), (5,6), (6,1), (6,2), (6,3), (6,4), (6,5), and (6,6). These are all equally probable. Of these, two pairs add up to 7, so the probability that the dice add up to 7 given that at least one of them came up six is $\frac 2{11}$.

b) This problem works out in much the same way as (a), with the same answer.

Remark. In fact, if the honest observer tells us that at least one die came up 1, or if he tells us that at least one die came up 2, or if he tells us that at least one die came up 3, or if he tells us that at least one die came up 4, then in each case, the conditional probability that the sum of the dice is 7 given the observer’s report is $\frac 2{11}$. Of course, the honest observer can always make one of these six reports.

Yet, if the observer tells us nothing, then the probability that the sum of the dice is 7 is $\frac 6{36}$, which is less than $\frac 2{11}$. There is a paradox: it appears that the observer can always lead us to conclude that the probability of having rolled a 7 is $\frac 2{11}$, even though the observer can’t influence the actual result of the die roll. How can this paradox be explained?

7.3 #4

Let $O$ be the event “Ann picks an orange ball”. Let $E$ be the event “Ann picks the second box”. We know that $p(E)=\frac 12$ and $p(O~|~E)=\frac 5{11}$ and $p(O~|~\overline E)=\frac 37$. We want $p(E~|~O)$. By Bayes’ Theorem, \begin{align*} p(E~|~O) &= \frac{p(O~|~E)p(E)}{p(O~|~E)p(E)+p(O~|~\overline E)p(\overline E)} \\ &= \frac{\frac 5{11}\cdot\frac 12}{\frac 5{11}\cdot\frac 12+\frac 37\cdot\frac 12} \\ &= \frac{35}{68}. \end{align*} The probability that Ann picked from the second box is $\frac{35}{68}$.

7.3 #6

Let $O$ be the event “player tests positive”. Let $E$ be the event “player takes steroids”. We know that $p(E)=0.05$ and $p(O~|~E)=0.98$ and $p(O~|~\overline E)=0.12$. We want $p(E~|~O)$. By Bayes’ Theorem, \begin{align*} p(E~|~O) &= \frac{p(O~|~E)p(E)}{p(O~|~E)p(E)+p(O~|~\overline E)p(\overline E)} \\ &= \frac{(0.98)(0.05)}{(0.98)(0.05)+(0.12)(0.95)} \\ &\approx 0.301. \end{align*} The probability that a player who tests positive is taking steroids is about $30.1\%$.

7.3 #16(b)

Let $O$ be the event “Ramesh is late”. Let $E_1$ be the event “Ramesh drove his car”, let $E_2$ be the event “Ramesh took the bus”, and let $E_3$ be the event “Ramesh rode his bike”. Then we know $p(E_1)=0.3$, $p(E_2)=0.1$, $p(E_3)=0.6$, $p(O~|~E_1)=0.5$, $p(O~|~E_2)=0.2$, and $p(O~|~E_3)=0.05$. By the generalized version of Bayes’ Theorem (page 472), \begin{align*} p(E_1~|~O) &= \frac{p(O~|~E_1)p(E_1)}{p(O~|~E_1)p(E_1)+p(O~|~E_2)p(E_2)+p(O~|~E_3)p(E_3)} \\ &= \frac{(0.5)(0.3)}{(0.5)(0.3)+(0.2)(0.1)+(0.05)(0.6)} \\ &= 0.75. \end{align*} There is a $75\%$ chance that Ramesh drove.