These problems are part of the homework due on Monday, July 28.
- Determine the largest integer $n$ that can’t be written as $5s+7t$, where $s$ and $t$ are nonnegative integers. Prove your answer, i.e., show that your $n$ can’t be written in this form and show that all larger integers can be written in this form.
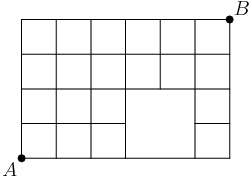
- How many paths are there from point A to point B in the grid below, if we can only travel along the lines going north (up) and east (right)? Be sure to notice the “gap” in the grid.
- Determine how many ways 8 indistinguishable objects can be distributed to 4 indistinguishable boxes. List the ways.
- Determine how many ways 8 distinguishable objects can be distributed to 4 indistinguishable boxes. Hint: Solve problem 3 first.