1. Melitta
   Hint

   Your parents probably have some of these in a cabinet. When in use, they are approximately conical.
2. Zildjian
   Hint

   You might see a Zildjian product on stage—at a concert or a comedy show.
3. Hagoromo
   Hint

   This brand is highly coveted by mathematicians.

You have a delicious cake whose top is covered with frosting. You're feeling hungry, so you cut yourself a nice 200-degree "slice" of cake (yes, that's five-ninths of the cake… so what?). But then, for reasons known only to yourself, you decide to turn that 200-degree wedge upside down and return it to its place, with the frosting now on the bottom.

We are going to pretend that the frosting sticks to the cake instead of coming off on the plate. Oh, and the cake magically fuses back together whenever you put back a slice. It's a special cake.

Not content with the amount of fun you've had so far, you then cut a new 200-degree slice, adjacent to the first (see figure below).

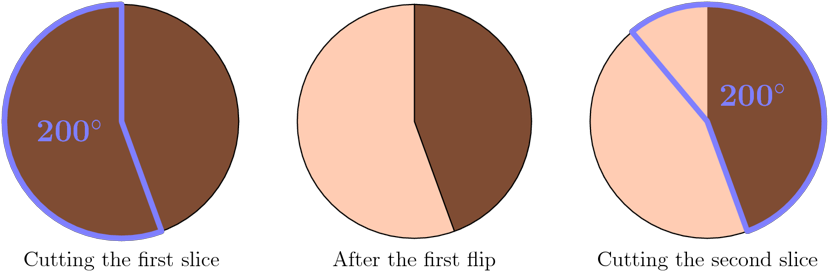
You turn this slice upside down and put it back, just like the first. You keep doing this (continuing counterclockwise around the cake). You are a strange person, but whatever makes you happy…

Eventually all the frosting is on top again! You have succeeded in your weird mission and now devour the entire cake in triumph! How many times did you cut a slice and turn it over?

Solution

No foolin': the answer is 4.

The tricky thing is to realize that when you turn a piece of cake upside down, you really do turn it. Thus, in the diagram above (which shows a top view of the cake), the colors in the turned sector are not only swapped, but also reversed left to right.

200° is not very special—the answer to this puzzle is the same for any angle greater than or equal to 180° (and less than 360°). However, Graham asks what the answer is for 7° slices. (Tip: Don't try that on an empty stomach.)

I got this puzzle from a post on Gil Kalai's blog. The post was written by Stan Wagon, but he got the puzzle from a Russian math contest. If you got this right, take a bow. Gil's original post included a poll—a multiple-choice poll with the correct answer included in the options—and only 9% of his readership (people who like reading about graph theory and quantum computing) chose correctly.

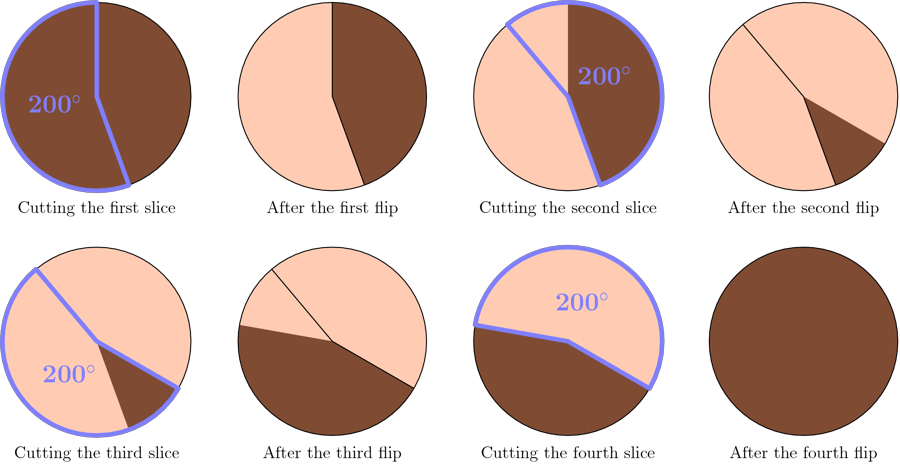
Congratulations to yesterday's solvers Trent, Atticus, and (breaking the streak of people with the same first names as members of Nine Inch Nails) Andrew and Graham. Thanks to everybody who made a guess!