Graded: Supplemental #1, 7.2 #10
Author Archives
Austin Shapiro
Solutions (6.3 to 6.5)
Graded: 6.3 #24, 6.4 #22
Notes on partitions
Part of today’s lesson was a departure from the textbook. Here are my lecture notes. (Note that these are just the “cues” I use in class, which are designed primarily for my own use. They don’t go into full detail and aren’t a good substitute for being in class, but they’re better than nothing.)
Supplemental problems for Homework 9
These problems are part of the homework due on Monday, July 28.
- Determine the largest integer $n$ that can’t be written as $5s+7t$, where $s$ and $t$ are nonnegative integers. Prove your answer, i.e., show that your $n$ can’t be written in this form and show that all larger integers can be written in this form.
- How many paths are there from point A to point B in the grid below, if we can only travel along the lines going north (up) and east (right)? Be sure to notice the “gap” in the grid.
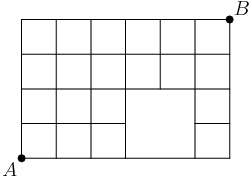
- Determine how many ways 8 indistinguishable objects can be distributed to 4 indistinguishable boxes. List the ways.
- Determine how many ways 8 distinguishable objects can be distributed to 4 indistinguishable boxes. Hint: Solve problem 3 first.
Solutions (5.2 to 6.2)
Graded: 5.2 #12, 5.3 #12
Solutions (4.4 to 5.1)
Graded: 5.1 #10, #22
Solutions to Midterm 1
Solutions to Midterm 1 are available. The median score was 77.5.
Please review the grading policy on the syllabus. I have added information about what numerical grades translate to A’s, B’s, C’s, and D’s.
Logic puzzle
If you want to test your propositional logic skills, try this puzzle that arose from a conversation at my office hours:
Suppose we are given the premises (1) $p\to q$ and (2) $\neg p\to q$.
a) What can we infer from (1) and (2)?
b) The contrapositive of (1) is $\neg q\to\neg p$. Putting that together with (2), we can infer $\neg q\to q$. Is that a contradiction? Why or why not?
Answers below…
Solutions (4.2 to 4.4)
Graded: 4.2 #32, 4.4 #8
Midterm information
The first midterm will be this Friday, July 11, from 2:00 to 3:00 in 4 Evans. We’ll start as close to 2:00 as possible, not at 2:10.
The only items you will need (and the only items that are allowed) are pens/pencils, erasers, and pencil sharpeners. You don’t need to bring a blue book; paper will be provided. No notes, books, or electronics may be used during the test.
This midterm will cover sections 1.1, 1.3-1.8, 2.1-2.5, and 4.1-4.4. The second hour of class on Thursday is reserved for review, and I encourage you to visit office hours if you want additional help. (The schedule is on the syllabus page.)
Sample midterms:
- Prof. Williams’ Spring 2014 sample midterm (solutions).
- Prof. Haiman’s Fall 2012 test (solutions). Problem #5 is out of bounds.
- Prof. Sturmfels’ Spring 2012 test (solutions). Problems #3, 4 are out of bounds.
- Prof. Sturmfels’ Spring 2010 test (solutions). Problems #1, 3 are out of bounds.
The timing and selection of topics in Math 55 has varied from term to term; problems listed as “out of bounds” above would not appear on our first midterm. In general, problems on the midterm will resemble problems that have been assigned as homework.